
 
 |

 
 |
 |
| prof. Stefan Banach w wieku 44 lat, Lwów 1936 |
| [Zdjęcia ze zbiorów prywatnych rodziny Banachów udostępniła Pani prof. Alina Filipowicz-Banachowa.] |
 |
| prof. Stefan Banach w wieku 52 lat, Lwów 1944 |
| [Zdjęcie ze zbiorów prywatnych rodziny Banachów udostępniła Pani prof. Alina Filipowicz-Banachowa.] |
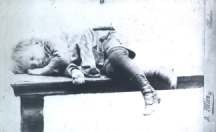 |
| Trzyletni Stefan Banach na Krakowskich Plantach. |
| [Zdjęcie wykonane przez Juliusza Miena ze zbiorów prywatnych rodziny Banachów udostępniła Pani prof. Alina Filipowicz-Banachowa.] |
,, Istnieją dokumenty stwierdzające, że Banach należał do bardzo pilnych uczniów, co w kategorii geniuszy jest dosyć rzadkie. A trzeba wiedzieć, że ówczesny program nauczania uwzględniał przede wszystkim łacinę, grekę, języki nowożytne, natomiast mniejszą wagę przykładano do przedmiotów ścisłych. Banacha posłano do szkoły, kiedy była ona typowym gimnazjum klasycznym. Program więc nie pokrywał się ani ze zdolnościami, ani z zainteresowaniami Banacha. Matematyki nauczali ludzie nie zawsze kompetentni. Banach we wspomnieniach o gimnazjum źle wyrażał się o poziomie i sposobie nauczania ulubionego przedmiotu. Zachowało się szczególnie dużo dokumentów dotyczących pobytu Banacha w drugiej klasie cesarsko-królewskiego Gimnazjum IV. Ciekawe - a dla licznych u nas reformatorów szkolnych być może nawet pożyteczne będzie prześledzenie planu nauki ówczesnych gimnazjalistów. Plan ten (w klasie II) przedstawiał się następująco: Religia, 2 godziny tygodniowo. Dzieje Starego Zakonu. Język łaciński, 8 godzin tygodniowo. Uzupełnienie nauki z klasy I o formach prawidłowych i nieodmiennych częściach mowy. Najważniejsze formy nieprawidłowe. Składnia najpospolitszych zdań pobocznych. Ćwiczenia ustne i pamięciowe jak w kl. I. Co miesiąc 3 zadania szkolne, 1 domowe. Język polski, 3 godziny tygodniowo. Z gramatyki: Powtórzenie o zdaniu materiału przerobionego w kl. I. Zdanie złożone, rodzaje zdań pobocznych. Uzupełnienie interpunkcji i ortografii. Czytanie wypisów, deklamacja. Wypracowania stylistyczne 3 razy na miesiąc, na przemian domowe, szkolne. Język niemiecki, 5 godzin tygodniowo. Rozmówki w formie pytań i odpowiedzi na podstawie czytanych ustępów, retrowersja, uczenie się na pamięć wyrazów, zwrotów i całych ustępów. Powtórzenie odmiany regularnej i głównych zasad składni. Co tydzień zadanie, z tych jedno domowe na miesiąc. Historia i geografia, 4 godziny tygodniowo. Dzieje starożytne zwłaszcza Grecji i Rzymu sposobem biograficznym. Geografia fizyczna i polityczna Azji i Afryki. Poziomy i pionowy układ Europy. Szczegółowa geografia Europy południowej i Wielkiej Brytanii. Ćwiczenia w rysowaniu szkiców kartograficznych. Matematyka, 3 godziny tygodniowo. Powtórzenie i uzupełnienie o najwyższym wspólnym podzielniku i najmniejszej wspólnej wielokrotności. Systematyczna nauka o ułamkach zwyczajnych. Zamiana ułamków zwyczajnych na dziesiętne i odwrotnie. Stosunki, proporcje. Reguła trzech pojedynczych z zastosowaniem proporcji. Wnioskowanie. Rachunek procentu pojedynczego. Z geometrii: osie symetrii dłużni i kątów, przystawanie trójkątów i zastosowanie tegoż. Najważniejsze właściwości koła, czworoboków i wieloboków. Ćwiczenia i zadania jak w klasie I. Historia naturalna, 2 godziny tygodniowo. Przez pierwsze 6 miesięcy zoologia: ptaki, gady, płazy, ryby, skorupiaki i robaki, mięczaki, szkarłupnie, jamochłony i pierwotniaki. Od marca świat roślinny. Były również przedmioty nadobowiązkowe: historia kraju rodzinnego, język francuski (na który wg statystyki szkolnej żaden z uczniów II klasy nie uczęszczał), śpiew, rysunki, kaligrafia, gimnastyka, stenografia."Tradycją krakowskich gimnazjów było utrzymywanie ścisłych kontaktów z instytucjami naukowymi, takimi jak Uniwersytet Jagielloński i Polska Akademia Umiejętności. Nauczyciele akademiccy i członkowie Komisji Akademii Umiejętności często uczyli w gimnazjach, a tym samym wprowadzali do nich standardy akademickie. Potwierdzają to katalogi świadectw klas od I do VII oraz protokół główny egzaminu dojrzałości c.k. Gimnazjum IV w Krakowie (Archiwum Państwowe w Krakowie sygn. 29/1434/2,3,4,5,6,7,37). Możemy w nich znaleźć informację, że nauk przyrodniczych udzielał Roman Gutwiński (1860-1932), polski botanik, algolog (badacz glonów), współtwórca polskiej algologii, a rysunków uczył znany artysta malarz Sylweryusz Saski (1863-1954). Po latach Banach stwierdził, że jego zainteresowania matematyczne rozwinął nauczyciel matematyki i fizyki w IV Gimnazjum, dr Kamil Kraft (1873-1945), który jednocześnie był pracownikiem naukowym katedry fizyki doświadczalnej Uniwersytetu Jagiellońskiego. W klasie maturalnej matematyki i fizyki uczył Stanisław Ziobrowski, profesor szkół średnich, jeden z pierwszych członków Towarzystwa Matematycznego w Krakowie (1919). Od roku szkolnego 1908/1909 dyrektorem IV Gimnazjum, po Antonim Pazdrowskim, był Roman Zawaliński (1855-1932), znany językoznawca, pedagog i etnograf. Katalogi IV Gimnazjum obrazują również, w jak złożonych warunkach osobistych Stefan Banach dorastał. Dane osobowe ucznia odzwierciedlają jego niejasną sytuację rodzinną. W rubrykach dotyczących danych osobowych ucznia w klasie od I do IV wpisany jest Juliusz Mien jako opiekun. Franciszka Płowa w klasie I i II widnieje jako matka, ale już w następnych klasach jedynie jako utrzymująca stancję, u której uczeń mieszka. Stopnie uzyskane z poszczególnych przedmiotów świadczą o tym, że Banach w klasach od I do IV był jednym z najlepszych uczniów. Gdy jesienią roku 1905 umiera Juliusz Mien, Stefan Banach jest w IV klasie gimnazjum i ma dopiero 13 lat. Po śmierci Miena w miejsce opiekuna zostaje wpisany Stefan Greczek. Na świadectwie ukończenia klasy IV pojawiają się pojedyncze oceny dostateczne, które coraz częściej występują w klasach VI-VII. Jednak matematyka i fizyka wiodą prym w jego zainteresowaniach i w klasie VII, a następnie maturalnej uzyskuje z tych przedmiotów oceny bardzo dobre z odznaczeniem. Z uzyskanych dokumentów wynika, że ze wszystkich przedmiotów, jakich uczył się w szkole, najbardziej upodobał sobie matematykę, która stała się jego pasją życiową - pracą, zabawą, rozrywką intelektualną. W klasie maturalnej wyniki zdecydowanie ulegają poprawie i Stefan Banach w pierwszym i drugim półroczu uzyskuje tylko dwie oceny dostateczne, a z pozostałych przedmiotów otrzymuje oceny dobre i bardzo dobre. W roku 1910 dnia 9 czerwca przed południem Stefan Banach przystąpił do egzaminu dojrzałości. Egzamin maturalny obejmował przedmioty z następującymi tematami: Język polski: Młodość Irydyona na Chiarze - jego rola i anal. postacie. Język grecki: Platon, Menon, o Sofistach. Dzieje ojczyste: Stosunki wymienione w Monarchii Histor. uzasadnienie. Matematyka: Ułożyć równania wszystkich linii krzywych przechodzących przez punkty A(4, 3), B(-4, 3), C(-4, -3), D(4, -3) i zbadać stosunek prostej y = (4/3)x do każdej z nich (pogląd ogólny). Egzamin maturalny zakończył się 13 czerwca 1910 roku i Komisja Egzaminacyjna orzekła, że Stefan Banach pomyślnie zdał egzaminy z wynikiem "dojrzały jednomyślnie". Kolegami gimnazjalnymi Banacha byli: Witold Wilkosz (1891-1941), przyszły matematyk i Marian Albiński (1891-1978) - to dzięki jego wspomnieniom możemy czerpać wiedzę o tamtych czasach. Albiński uczęszczał do tej samej klasy, co Banach w latach 1902-1906. Albiński przeniósł się jednak do gimnazjum Sobieskiego z powodów, które dają nam obraz stosunków panujących w szkole w tamtych czasach. Zgodnie z tym, co pisze Albiński, w piątej klasie zmienił on szkołę, ponieważ nauczyciel greki ocenił go niesprawiedliwie, wystawiając mu ocenę niedostateczną na półrocze. W szkołach będących w zaborze austro-węgierskim ocena niedostateczna wiązała się z koniecznością zapłaty grzywny w wysokości 20 koron. Marian Albiński wspomina:
,,Wraz ze mną przeniósł się do Gimnazjum Sobieskiego również Wilkosz, nie wiem z jakiego powodu. Banach pozostał w Gimnazjum IV, aż do złożenia matury w roku 1910. Po opuszczeniu gimnazjum "u Goetza" moja łączność z Banachem zerwała się, natomiast Wilkosz nadal utrzymywał z Banachem bliskie kontakty, a ja przyjaźniłem się z Wilkoszem i widywałem ich niejednokrotnie razem. Stefan Banach, jakim go pamiętam, był chłopcem spokojnym, niepozbawionym jednak łagodnego humoru, dobrym kolegą. Miał naturę skrytą. Był zawsze w czystym, porządnym mundurku, jak my wszyscy, nie znać było na jego twarzy zmizerowania czy wygłodzenia, choć zmuszony skromnymi warunkami materialnymi dawał płatne korepetycje młodszym kolegom szkolnym, a także tzw. korepetycje "na mieście"; współkolegom z klasy pomagał bezinteresownie.Już od najniższych klas łączyła Banacha i Wilkosza miłość do matematyki. Na tzw. pauzach często widziałem ich rozwiązujących zagadnienia matematyczne, które dla mnie jako humanisty były po prostu chińszczyzną. Przyjaźń Banacha z Wilkoszem nie ograniczała się tylko do terenu szkoły, spotykali się po lekcjach w domu Wilkosza przy ul. Zwierzynieckiej lub w budynku szkolnym i na Plantach Krakowskich. W czasach późniejszych bodaj pół nocy trwało odprowadzanie się zacietrzewionych studentów - Banacha i Wilkosza - po ulicach Krakowa, gdy jakaś kwestia zajęła ich umysły. Nie brałem udziału w tych matematycznych rozmowach, ale prowadziłem nieraz długie dysputy z samym Wilkoszem, z którym byłem bardziej zżyty. Łączyły nas w gimnazjum i po maturze zainteresowania literackie i słabość do tych samych studentek."W roku 1910, po maturze, drogi Stefana Banacha i Witolda Wilkosza rozeszły się na kilka lat. Witold Wilkosz egzamin dojrzałości zdał w 1910 roku w III Gimnazjum w Krakowie i rozpoczął studia początkowo filologiczne, później matematyczne na Wydziale Filozoficznym Uniwersytetu Jagiellońskiego, gdzie po latach został profesorem.
  |
| prof. Hugo Steinhaus |
,, Idąc letnim wieczorem 1916 roku wzdłuż Plant, usłyszałem rozmowę, a raczej tylko kilka słów; wyrazy "całka Lebesgue'a" były tak nieoczekiwane, że zbliżyłem się do ławki i zapoznałem z dyskutantami: to Stefan Banach i Otto Nikodym rozmawiali o matematyce. Powiedzieli mi, że mają jeszcze trzeciego kompana, Wilkosza."Spotkanie Steinhausa i Banacha miało niemal natychmiastowe konsekwencje naukowe i zaowocowało wieloletnią współpracą i przyjaźnią. Pierwsza publikacja Banacha, napisana wspólnie ze Steinhausem, opublikowana w "Biuletynie Akademii Krakowskiej" w 1919 roku, nosiła tytuł: Sur la convergence en moyenne de séries de Fourier (O zbieżności w przeciętnej szeregu Fouriera).
 |
| Stefan Banach w wieku 27 lat. Kraków 1919 rok. |
| [Zdjęcie ze zbiorów prywatnych rodziny Banachów udostępniła Pani prof. Alina Filipowicz-Banachowa.] |
 |
| prof. Wacław Sierpiński |
|
|
 |
| Łucja Braus-Banachowa. |
| [Zdjęcie ze zbiorów prywatnych rodziny Banachów udostępniła Pani prof. Alina Filipowicz-Banachowa.] |
 |
| prof. Stanisław Mazur |
,, Ale rok 1922, w którym Stefan Banach w polskim czasopiśmie Fundamenta Mathematicae ogłosił swą rozprawę doktorską pt. Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales, jest datą przełomową w historii matematyki XX wieku. Ta kilkudziesięciostronicowa rozprawa ugruntowała bowiem ostatecznie podstawy analizy funkcjonalnej, nowej dyscypliny matematycznej, która - jak to wykazały rezultaty badań Stefana Banacha i innych - posiada kapitalne znaczenie dla dalszego rozwoju nie tylko samej matematyki, ale również nauk przyrodniczych, a w szczególności fizyki."
 |
 |
| Uniwersytet Jana Kazimierza - obecnie im. Iwana Franki. [fot. Nikodem Miranowicz] |
 |
| Patriae decori civibus educandis (Sentencia in frontis almae mater miae). [fot. Nikodem Miranowicz] |
 |
| Stary gamach Uniwersytetu Jana Kazimierza, ul. św. Mikołaja 4. |
| [Zdjęcie ze zbiorów prywatnych rodziny Riedlów udostępnił Pan prof. Tadeusz Riedl.] |
,, Banach nie tylko nie skończył studiów, ale i doktorem został w sposób dość niezwykły. Gdy rozpoczął pracę we Lwowie, był już autorem wielu doniosłych rezultatów i wciąż uzyskiwał kolejne. Jednak na uwagi, że powinien wkrótce przedstawić pracę doktorską, odpowiadał, że ma jeszcze czas i może wymyślić coś lepszego, niż to, co osiągnął do tej pory. W końcu więc zwierzchnicy Banacha zniecierpliwili się. Ktoś spisał najnowsze rezultaty jego pracy, co zostało uznane za znakomitą pracę doktorską. Przepisy jednak wymagały również egzaminu. Pewnego dnia zaczepiono Banacha na korytarzu Uniwersytetu Jana Kazimierza: "Czy mógłby pan wpaść do dziekanatu, są tam jacyś ludzie, którzy mają pewne problemy matematyczne, a pan na pewno potrafi im wszystko wyjaśnić". Banach udał się zatem do wskazanego pokoju i chętnie odpowiedział na wszystkie pytania, nieświadom tego, że właśnie zdaje egzamin doktorski przed komisją specjalnie w tym celu przybyłą z Warszawy. Dziś prawdopodobnie doktoratu w ten sposób uzyskać nie można..."W czerwcu 1922 roku Banach habilitował się, a już w lipcu otrzymał nominację na profesora nadzwyczajnego Uniwersytetu Lwowskiego i następnie został powołany na kierownika II Katedry Matematyki Wydziału Matematyczno-Fizycznego. Funkcję kierownika katedry pełni do 1939 roku. Dwa lata później Polska Akademia Umiejętności powołuje Banacha na swojego członka korespondenta. W roku akademickim 1924/25 otrzymał roczny, płatny urlop naukowy i wyjechał do Paryża jako stypendysta Rządu RP.
 |
| Od lewej żona prof. Stefana Banacha - Łucja Banach, prof. Stefan Banach z synem Stefanem. Marsylia 1925 rok. |
| [Zdjęcie ze zbiorów prywatnych rodziny Banachów udostępniła Pani prof. Alina Filipowicz-Banachowa.] |
 |
| Łucja Banach z synem Stefanem. Marsylia 1925 rok. |
| [Zdjęcie ze zbiorów prywatnych rodziny Banachów udostępniła Pani prof. Alina Filipowicz-Banachowa.] |
 |
 |
 |
| prof. Kazimierz Kuratowski |
,, Do szczególnie ważnych wydarzeń dla matematyki polskiej zaliczyć należy powołanie do życia w 1931 roku "Monografii Matematycznych". Fakt ten oznaczał nowy etap w rozwoju Polskiej Szkoły Matematycznej. Etap wcześniejszy, który można nazwać pionierskim, charakteryzował się produkcją niemal wyłącznie krótkich publikacji, zawierających nowe wyniki (drukowane przede wszystkim w "Fundamentach i Studiach"). Nadszedł jednak czas na syntezę osiągnięć polskich matematyków bądź na syntezę całych dyscyplin matematycznych, do których Polacy wnieśli szczególnie duży wkład. Wstępny plan przewidywał wydanie monografii obejmujących analizę funkcjonalną (I tom - Opérations linéaires Banacha), teorię całki (II tom - Théorie de l'intégrale Saksa), topologię (III tom - autora niniejszego opracowania), hipotezę continuum (IV tom - Sierpińskiego), teorię szeregów trygonometrycznych (V tom - Zygmunda), teorię szeregów ortogonalnych (VI tom - KALEN Steinhausa i Kaczmarza). W krótkim czasie "Monografie Matematyczne" zdobyły sobie pozycję wśród najpoważniejszych seryjnych wydawnictw naukowych."Jako dopełnienie swojej działalności dydaktycznej Banach zaczął pisać podręczniki akademickie: Rachunek różniczkowy i całkowy, tomy I i II, które zostały wydane odpowiednio w latach 1929 i 1930, natomiast następne tomy I i II, pt.Mechanika w zakresie szkół akademickich, ukazały się w roku 1938. Podręczniki powyższe oraz podręczniki dla szkół średnich, napisane wspólnie z Włodzimierzem Stożkiem i Wacławem Sierpińskim, miały zaradzić trudnej sytuacji materialnej Banacha w owym czasie. Steinhaus napisał:
,, Banach umiał pracować zawsze i wszędzie. Nie był przyzwyczajony do wygód i nie potrzebował komfortu, więc pensja profesorska powinna mu była wystarczyć. Ale zamiłowanie do życia kawiarnianego i zupełny brak mieszczańskiej oszczędności oraz regularności w sprawach codziennych wpędziły go w długi, a w końcu w sytuację bardzo trudną. Chcąc z niej wyjść, zabrał się do pisania podręczników."Ze wspomnień Turowicza wiemy, że dopiero pomoc udzielona przez profesora Benedykta Fulińskiego (1881-1941), który stał się gwarantem jego długów, przyniosła konkretne rozwiązanie. Dochody z napisanych podręczników pozwoliły Banachowi na częściowe spłacanie długów. Prawdopodobnie nagroda Polskiej Akademii Umiejętności otrzymana w 1939 roku w wysokości 20 000 zł zlikwidowała je ostatecznie. Rezultaty badań matematycznych osiągnięte przez Banacha budziły wielkie zainteresowanie międzynarodowego środowiska matematycznego. W roku 1936 zaproponowano Banachowi jeden z odczytów plenarnych na Międzynarodowym Kongresie Matematycznym w Oslo. Wygłosił wówczas wykład pt. Die Theorie der Operationen und ihre Bedeutung für die Analysis ("Teoria operacji i jej znaczenie w analizie"). Do Lwowa przyjeżdżali naukowcy zarówno z Polski, jak i zagranicy. Wśród nich byli przedstawiciele polskich środowisk matematycznych, m.in. z Warszawy (Wacław Sierpiński, Karol Borsuk, Stefan Mazurkiewicz, Alfred Tarski) i Wilna (Antoni Zygmund), a wśród gości zagranicznych przedstawiciele Austrii (Mojżesz Jacob), Czechosłowacji (Wacław Hlavaty), Francji (Emil Borel, Maurice Fréchet, Henri Lebesgue, Paul Montel), Danii (Axel Andersen), Niemiec (Leon Lichtenstein, Ernst Zermelo), Rumunii (Pierre Segrescu, Simion Stoilow), Stanów Zjednoczonych (John von Neumann), Szwajcarii (Rolin Wavre), Wielkiej Brytanii (A. Cyril Ofiord, A. J. Ward), czy Związku Sowieckiego (Paweł S. Aleksandrow, Nina Bari, Nikołaj N. Bogolubow, Łazar A. Lusternik, Nikołaj Łuzin, Dymitr Mienszow, Siergiej Ł. Sobolew i inni). Chociaż analiza funkcjonalna i teoria miary stały się głównymi dziedzinami pracy naukowej Banacha, które przyniosły mu największą sławę, to jednak wniósł on niemały wkład i w inne działy matematyki, takie jak: teoria funkcji rzeczywistych, teoria szeregów ortogonalnych czy opisowa teoria mnogości. Paradoks Banacha-Tarskiego jest jednym z najbardziej znanych wyników w teorii mnogości. Został odkryty przez Banacha wspólnie z Alfredem Tarskim (1902-1983) i opublikowany w pracy Sur la décomposition des ensembles de parties respectivement congruentes (O rozkładzie zbiorów punktów na części odpowiednio przystające), zamieszczonej w VI tomie Fundamenta Mathematicae. Autorzy tego artykułu, opublikowanego w 1924 roku, odkryli, że stosując oryginalne operacje, można dokonać takiego rozkładu kuli na części składowe, które później ponownie scalone dadzą dwie kule identyczne z tą pierwotną.
 |
| prof. Stanisław Ulam |
,,A była nawet sesja, która trwała 17 godzin - jej rezultatem był dowód pewnego ważnego twierdzenia z przestrzeni Banacha, ale nikt go nie zapisał i nikt już dziś nie zdoła go odtworzyć, gdyż - jak pisze Hugo Steinhaus - prawdopodobnie blat stolika pokryty śladami chemicznego ołówka został, jak zwykle, zmyty przez sprzątaczkę. Taki był niestety los niejednego twierdzenia udowodnionego przez Banacha i Jego uczniów. Na podstawie zachowanych przekazów można wysnuć wniosek, że dla uczestników dyskusji w Kawiarni Szkockiej rozwiązywanie problemów matematycznych nie było pracą, lecz przyjemnością."

 |
| W tym budynku mieściła się Kawiarnia Szkocka, obecnie w lokalu tym jest bank. [fot. Nikodem Miranowicz] |
 |
| Stanisław Mazur i Stanisław Ulam |
,,Sądzę, że te wielogodzinne kawiarniane dyskusje z Banachem, a częściej z Banachem i Mazurem, były czymś unikalnym. Nigdzie i nigdy nie zdarzyło mi się nic, co by przewyższało, dorównywało lub choćby zbliżało się do skali i natężenia naszej ówczesnej współpracy - z wyjątkiem być może Los Alamos w latach wojny."W 1936 roku Stanisław Mazur, również bywalec kawiarni "Szkockiej", postawił pewien problem dotyczący przestrzeni Banacha. Nagrodą za jego rozwiązanie miała być żywa gęś. Rozwiązanie podał w 1972 roku, czyli po 36 latach, szwedzki matematyk Per Enflö, który z rąk prof. S. Mazura odebrał obiecaną nagrodę w Centrum im. Stefana Banacha w Warszawie.
 |
| prof. Stanisław Mazur i dr Per Enflö [fot. Danuta Rago] |
 |
| Stefan Banach jr, student medycyny 1942 rok. |
| [Zdjęcie ze zbiorów prywatnych rodziny Banachów udostępniła Pani prof. Alina Filipowicz-Banachowa.] |
 |
| dr Stefan Banach jr z żoną Aliną z d. Filipowicz i młodszą córką Kasią |
 |
| dr Stefan Banach jr z żoną Aliną Filipowicz-Banachową |
 |
| Nominacja profesorska w Belwederze Aliny Filipowicz-Banachowej, obok mąż dr n. med. Stefan Banach jr |
 |
| dr n. med. neurochirurg Stefan Banach jr |
 |
| Iwona Banach-Suchowierska - starsza córka dr. Stefana Banacha jr., wnuczka prof. Stefana Banacha |
 |
| Joachim Stefan Suchowierski - syn Iwy Banach-Suchowierskiej, prawnuk prof. Stefana Banacha |
 |
| Kasia Banach młodsza córka dr. Stefana Banacha jr. z córkami |
 |
| Georgia i Audrey Salas - córki Kasi Banach, prawnuczki prof. Stefana Banacha |
| [Zdjęcia ze zbiorów prywatnych rodziny Banachów udostępniła Pani prof. Alina Filipowicz-Banachowa.] |
,, Stała się ona Księga Szkocka relikwią i największą świętością dla polskich matematyków. Jej kopie krążą po świecie, lecz oryginał pokazywany jest nader rzadko. We Wrocławiu, ktoś za sprawą Steinhausa kupił nowy brulion. Pod nazwą Nowej Księgi Szkockiej. Prowadzony w latach 1946-1948 był zbiorem problemów i rozwiązań. Spełniał tę samą rolę, co jego poprzednik ze Lwowa. Opieka nad Księgą Wrocławską była w gestii profesorów Marczewskiego i Steinhausa. Tradycja Księgi Szkockiej trwała więc nadal. Jednak brulionowi założonemu we Wrocławiu brak było tego mitu i legendy, jaką charakteryzowała się Księga Szkocka: oryginalna, jedyna i niepowtarzalna."Na zlecenie Steinhausa Księga Szkocka została przepisana na maszynie. Następnie Ulam przetłumaczył Księgę na język angielski. W roku 1935 Ulam wyjechał do USA, ale utrzymywał kontakt z rodzinnym Lwowem. Zachowane listy Stefana Banacha do Ulama świadczą o nieprzerwanej współpracy tych uczonych aż do wybuchu II wojny światowej. W załączniku matematycznym. Stefan Banach przedstawił dwa fundamentalne twierdzenia "ukazujące na drodze matematycznej konieczności" kwantowania czasu w mechanice statystycznej. Podobnie można okazać konieczność kwantowania innych wielkości fizycznych. Nie wiadomo, jaka była wówczas waga tych wyników i na ile Banach wyprzedzał swoją epokę. John von Neumann, matematyk amerykański węgierskiego pochodzenia, przyjeżdżał do Polski w okresie międzywojennym trzykrotnie. Za każdym razem na osobiste polecenie Norberta Wienera, - ojca cybernetyki, usiłował namówić Stefana Banacha do emigracji do USA; po raz ostatni, był we Lwowie w roku 1937. W odpowiedzi na kolejną propozycję wyjazdu Banach spytał: a ile daje profesor Wiener? Przewidzieliśmy to pytanie - odparł zadowolony Amerykanin, sięgając do kieszeni. - Oto czek, na którym profesor Wiener wpisał jedynkę i złożył swój podpis. Proszę dopisać taką ilość zer, jaką pan uzna za stosowną! Banach pomyślał chwilę i powiedział: - To za mała suma, jak za opuszczenie Polski. I został, mimo że wojenne chmury nadciągały już nad Europę.
 |
| prof. John von Neumann |
,, A więc w 39 r. wojna zastała nas razem w Worochcie, która wtedy na skutek korekt granicznych była odległa o 2 godz. drogi od granicy węgierskiej. Mieliśmy parę tysięcy złotych z nagrody Rychter-Mościckiej (20 tys. zł). Reszta przepadła w P.K.O. Radziłem Rodzicom przejść granicę węgierską, a stamtąd dostać się dalej do USA. Jednak decyzja wówczas nie była łatwa, tak więc dostaliśmy się do Lwowa, który był już bombardowany z powietrza."Tuż po wybuchu II wojny światowej w 1939 roku Stefana Banacha nieoczekiwanie odwiedził ojciec, Stefan Greczek, wraz z przyrodnią siostrą Antoniną. Wizyta ta była bardzo miła, gdyż po raz pierwszy Stefan Banach został przedstawiony Antoninie jako jej brat. Działo się to na tle wydarzeń, o których pisze Stefan Banach jr:
,, Podczas dwóch lat okupacji sowieckiej ja skończyłem tzw. 10-tą klasę typu sowieckiego i złożyłem egzamin maturalny, a potem w r. 1940-1941 skończyłem pierwszy rok medycyny (profesorowie byli wszyscy ci sami); ojciec zaś wykładał i był kierownikiem katedry, która miała profesorów i w ten sposób pracowali tam ci, którzy schronili się z Warszawy: Saks, Knaster itd. Ojciec cieszył się popularnością - zresztą ten właśnie okres musi Pan Profesor znać od Hugona. Natomiast sytuacja nasza osobista zmieniła się diametralnie, gdy Lwów zdobyli Niemcy w 1941 r. Muszę wspomnieć, że Ojciec dwa dni przed wybuchem wojny niemiecko-rosyjskiej w 1941 został zaproszony na jakiś zjazd do Kijowa, pojechał tam, a gdy przybył, wybuchła wojna. Wsiadł natychmiast do ostatniego pociągu w kierunku Lwowa i już tuż przed zdobyciem go przez Niemców wrócił."Niemcy wkroczyli do Lwowa nocą z 30 czerwca na 1 lipca 1941 roku, w trzy dni po wycofaniu się Sowietów. Mieszkańcy Lwowa byli pod wstrząsającym wrażeniem zbrodni NKWD dokonanej na kilku tysiącach więźniów w więzieniach lwowskich. W dniu 2 lipca Niemcy aresztowali profesora Kazimierza Bartla z Politechniki Lwowskiej. Podczas nocy z 3/4 lipca SS i Gestapo aresztowało kolejną grupę, 22 profesorów uczelni lwowskich: Uniwersytetu, Politechniki i Akademii Weterynaryjnej. Wczesnym rankiem 4 lipca 1941 roku zostali oni wszyscy rozstrzelani na Wzgórzach Wuleckich. Stefan Banach z żoną uniknął losu swoich kolegów naukowców. Jego syn wspominał:
,, Zaczęła się heca, przed którą pochyliły się najpoważniejsze głowy. Ojciec i inni nie mogli już pracować. Zresztą pomordowano ich. Myślę, że ojca uchronili sami Ukraińcy za jego tolerancyjny stosunek do nich przed wojną. Mamę osobiście, oprócz niekłaniania się niektórych na ulicy (Taszycki), nie spotkało "właściwie żadne nieszczęście". Kulczyński własnoręcznie zrobił Matce fałszywe papiery."W okresie 1939-1945 polska szkoła matematyczna poniosła wielkie straty. Wielu matematyków zostało zamordowanych, a wśród nich: Herman Auerbach (1901-1942), Kazimierz Bartel (1882-1941), Max Eidelheit (1910-1943), Antoni Hoborski (1879-1940), Stefan Kaczmarz (1895-1939), Stefan Jan Kempisty (1892-1940), Michał Kerner (1902-1943), Mojżesz D. Kirszbraun (1903 lub 1904-1942), Stanisław Marian Kołodziejczyk (1907-1939), Adolf Lindenbaum (1901-1942), Antoni Łomnicki (1881-1941), Józef Marcinkiewicz (1910-1940), Aleksander Rajchman (1890-1940), Stanisław Ruziewicz (1889-1941), Stanisław Saks (1897-1942), Juliusz Paweł Schauder (1899-1943), Józef Schreier (1908-1942), Włodzimierz Stożek (1883-1941) i Zygmunt Zalcwasser (1898-1943). Jedynie Leon Chwistek (1884-1944), Samuel Dickstein (1851-1939), Stefan Mazurkiewicz (1888-1945), Witold Wilkosz (1891-1941) i Stanisław Zaremba (1863-1942) zmarli śmiercią naturalną. Stefan Banach jr wspominał los własnej rodziny:
,, (...) w końcu uciekłem do swego dziadka, górala, pod Nowy Targ na Podhalu w 1943 r. Przedtem pracowałem u p. Rudolfa Weigla, który był kierownikiem Instytutu Bakteriologicznego we Lwowie, gdzie karmiłem wszy i w ten sposób utrzymywałem przy życiu (kartofiami) całą naszą trójkę. Po mojej ucieczce ojciec zresztą również tam pracował, właśnie karmiąc klateczki z wszami."W czasie okupacji niemieckiej (1941-1944) Banach wraz z innymi pracownikami naukowymi, przedstawicielami kultury i członkami ruchu oporu, uczniami szkół gimnazjalnych i studentami znaleźli dość bezpieczne zajęcie jako karmiciele wszy w Instytucie Badań nad Tyfusem Plamistym profesora Rudolfa Weigla. Uczestniczyli oni w doświadczeniach, w których wymagane było karmienie wszy ludzką krwią. Ponieważ Niemcy byli bardzo zaangażowani w ten projekt z powodów wojskowych, dlatego uczestniczący w eksperymencie otoczeni byli specjalną ochroną, co pozwalało im unikać represji ze strony okupantów. Do czasu wybuchu II wojny światowej Zakład Biologii Uniwersytetu Jana Kazimierza na potrzeby Polskiego Ministerstwa Spraw Wojskowych produkował znaczne ilości szczepionki przeciwko tyfusowi. W okresie okupacji sowieckiej, od 22 listopada 1939, Zakład profesora Weigla został włączony do nowo powstałego Instytutu Sanitarno-Bakteriologicznego, a profesorowi Weiglowi polecono kontynuowanie produkcji szczepionki. Całość produkcji, prócz niewielkich ilości przeznaczonych na potrzeby cywilne, przekazywano Armii Czerwonej, którą w ten sposób zabezpieczano przed epidemią. W czerwcu 1941 roku, gdy armia Trzeciej Rzeszy zaatakowała Związek Sowiecki i wkroczyła do Lwowa, Instytut, a wraz z nim Zakład profesora Weigla, przemianowano na Institut fur Fleckfieber und Virusforschung. Niemiecki zarząd pozostawił Weigla na stanowisku dyrektora Instytutu, zlecając mu kontynuację badań i jednocześnie zwiększenie produkcji szczepionki, która tym razem w całości kierowana była do niemieckiej armii lądowej. Prace prowadzono w budynku dawnego Gimnazjum Królowej Jadwigi. Profesor Stefan Kryński wspomina rolę, jaką odegrał Instytut w ratowaniu polskich elit intelektualnych tamtego okresu:
,, Niezmiernie skomplikowana sytuacja, w jakiej znalazło się lwowskie środowisko uczelniane w lipcu 1941 roku, skłoniła Weigla do dalszego prowadzenia Instytutu. Widział w tym możliwość pomocy dla licznej rzeszy pozbawionych pracy profesorów i asystentów. Wymógł u Niemców prawo do całkowitej decyzji w doborze personelu, biorąc za niego pełną odpowiedzialność. Instytut zaczął wzrastać w postępie geometrycznym. Nie tylko środowisko uczelniane, ale również zagrożona wywozem do Niemiec, ucząca się i konspirująca młodzież, bojownicy ruchu oporu, których z Instytutem często łączyła tylko legitymacja, tworzyli razem jedyny w swoim rodzaju personel wytwórni szczepionek przeciw durowi plamistemu."Prof. Jerzy Chmielowski, który w 1944 roku jako maturzysta kompletów tajnego nauczania był zatrudniony w Instytucie Weigla, pisze:
,, Wielu już nie pamięta o twórcach prężnego ośrodka naukowego w przedwo jennym Lwowie. Ci, którzy pamiętają, mają obowiązek przypominać o profesorze Jakubie Parnasie - biochemiku, Stefanie Banachu - matematyku i wielu innych, którzy nadali środowisku lwowskiemu wymiar europejski. Należał do nich przede wszystkim profesor Rudolf Weigl, twórca szczepionki przeciw tyfusowi plamistemu. On pierwszy użył organizmu owada do hodowli riketsji nierozwijających się na zwykłych pożywkach mikrobiologicznych. Torował drogę współczesnym metodom wirusologii. Jako jedyny Polak był dwukrotnie nominowany do Nagrody Nobla w dziedzinie fizjologii i medycyny - której nigdy nie dostał z różnych powodów. Austriak z urodzenia, Polak z wyboru, w którym szczególne koleje życia, a potem klimat polskiej kultury ukształtowały poczucie narodowe i patriotyzm (...). W szczelnie zamkniętej drewnianej klatce wielkości pudełka zapałek z dnem z gazy młyńskiej umieszczano około 500 larw wszy odmierzanych objętościowo z cechowanej mikromenzurki oraz skrawek 1 cm2 tkaniny wełnianej. Owady przez gazę młyńską miały kontakt ze skórą karmiciela. Po odkażeniu skóry roztworem sublimatu w 60% alkoholu karmiciel umieszczał po 10 klatek przewiązanych pasem gumowym na każdej łydce (mężczyzna) lub udzie (kobieta). Karmienie krwią odbywało się codziennie przez 30 minut, po czym klatki umieszczano w termostacie (32°C)."Cykl hodowlany trwał około 12 dni. Jak wspomina prof. Jerzy Chmielowski:
,, Stefan Banach jako karmiciel hodował 20 klatek z 10 tys. wszy w każdym cyklu hodowlanym powtarzającym się przez wiele miesięcy."Banach pracował w Instytucie do końca okupacji niemieckiej Lwowa, czyli aż do lipca 1944 roku. Wiele lat później Stefan Banach syn relacjonował:
,, Ojciec odwiedził mnie w Krakowie, w tym okresie w 1944 r. był parę dni, wyglądał lepiej (...). Wówczas powiedział mi, że "przerzuca" się na zagadnienia fizyczne i ma idee, które powinny dać Mu nagrodę Nobla. Nasze pożegnanie było smutne i tchnęło beznadziejnością. Rzeczywistość zadała nam obu cios gorszy, niż mogliśmy się spodziewać, albowiem wówczas widziałem go po raz ostatni. I tu znowu ojciec w tym czasie wrócił właściwie przez front, gdyż w 2 tygodnie później bolszewicy odbili Lwów i szerokim frontem zbliżyli się do Warszawy i tam na kres prawie roczny stanęli. W ten sposób zostałem odcięty frontem od rodziców i przez rok nie miałem zupełnie żadnych od nich wiadomości. W 1945 roku po ponownej ofensywie rosyjskiej został zdobyty Kraków, a równocześnie dostałem pierwsze wiadomości o ojcu, że wraz z Mamą jest w Moskwie, że znowu jest profesorem itd. Poza tem ojciec ze swej strony poszukiwał mnie. Jednakże był to czas wojny. Chaos panował kompletny. Do Lwowa nie można było pojechać po prostu, gdyż panował stan wyjątkowy, no a także istniała faktyczna granica pod Przemyślem, tak że trzeba było starać się o formalny paszport polski i wizę rosyjską. Z rozmaitych oznak zorientowałem się, że szuka podstaw do opuszczenia na rzecz Polski i argumentów dostatecznych do zrezygnowania z zaszczytów, jakie ewentualnie czakałyby go w Związku Radzieckim, gdyby oświadczył oficjalnie, że chce tam pozostać. Jak się później dowiedziałem od Matki, w tych sprawach rozmawiano z Nią, oświadczając, że ojciec jest murowanym kandydatem do Nagrody Stalinowskiej (naukowej), jeśli zostanie tam. Tak więc nie wiedząc o tym, że Matka w tym czasie argumentuje tam podobnie, oświadczyłem w Krakowie, że studiuję medycynę (zgodnie z prawdą, gdyż tuż po uwolnieniu Krakowa zapisałem się na II rok medycyny), a ojciec zapewne zostanie zaproszony na U.J. na katedrę. Przedtem wyjaśniłem krakowskim matematykom w dyskrecji, o co chodzi, i ojciec został oficjalnie mianowany zaocznie profesorem zwyczajnym Uniwersytetu Jagiellońskiego w Krakowie. W czerwcu 1945 dowiedziałem się od p. Wasser-Wareckiego, że ojciec jest bardzo ciężko chory, że jest we Lwowie i że jeśli chcę w ogóle jeszcze zobaczyć, to radzi mi, abym nie bacząc na trudności i granice, natychmiast udał się do Lwowa. Mówił mi to na ulicy, w przypadkowym spotkaniu, z takim naciskiem i błyskiem w oczach, że to mnie zaalarmowało. Nie chciał poza tem nic więcej powiedzieć. Przez czerwiec, lipiec i sierpień bezskutecznie starałem się o paszport i wizę do Lwowa. Dopiero na skutek interwencji z drugiej strony, ze Lwowa otrzymałem z końcem sierpnia 1945 paszport i wyjechałem do Lwowa dnia 31 sierpnia, a przybyłem 2 września, w dniu naszych wspólnych z ojcem imienin. Jadąc z dworca do domu (na Dwernickiego), na Placu Bernardyńskim spojrzałem przypadkiem na gazetę trzymaną przez jakiegoś mężczyznę w ręku i zobaczyłem zdjęcie ojca w żałobnej ramce wraz z artykułem pośmiertnym. Zmarł 31 sierpnia, w dniu, w którym wyjeżdżałem z Warszawy. Ojca pogrzebałem dwa dni później. Był to ostatni oficjalny pogrzeb katolicki w mieście z przejściem konduktu przez miasto (z księdzem!). Było to życzenie mojej Matki, a władze sowieckie w tym wypadku były potulne. Pod Starym Uniwersytetem na Mikołaja przemawiał Nikliborc. Pochowałem ojca na cmentarzu Łyczakowskim, w obcym grobowcu rodziny Riedlów (tych od herbaty i kawy), w których kamienicy Rodzice mieli ostatnie mieszkanie."Ostatnie miesiące swojego życia ciężko chory Stefan Banach spędził pod pełną poświęcenia opieką Władysława Nikliborca, co wspominał Stefan Banach syn:
,, Nikliborc był tym, który szereg ostatnich miesięcy spełniał funkcję niańki wobec ojca i mej nieszczęśliwej Matki, opiekuna i chłopca na posyłki. Nie wiem skąd w tej małej postaci brało się tyle hartu i złotego serca."
 |
| prof. Stefan Banach, Lwów 1944 rok |
| [Zdjęcie ze zbiorów prywatnych rodziny Banachów udostępniła Pani prof. Alina Filipowicz-Banachowa.] |
 |
| Dom państwa Riedlów, w którym zmarł prof. Banach |
| [Zdjęcie ze zbiorów prywatnych rodziny Riedlów udostępnił Pan prof. Tadeusz Riedl.] |
  |
 |
| [Zdjęcia ze zbiorów prywatnych rodziny Riedlów. Udostępnił prof. Tadeusz Riedl.] |
 |
  |
| Medal Polskiej Akademii Nauk wybity w setną rocznicę urodzin Prof. Banacha. |
 |



 |
| Międzynarodowe Centrum Matematyczne im. S. Banacha i Instytut Matematyczny PAN przy ul. Śniadeckich 8 w Warszawie. |


 |
| Popiersie Stefana Banacha w Międzynarodowym Centrum Matematycznym. |
 |
 |
| Pomnik Stefana Banacha przed budynkiem Instytutu Matematyki i Fizyki Uniwersytetu Jagiellońskiego przy ul. Reymonta 4. |
 |
| Płaskorzeźba Stefana Banacha i witraż autorstwa Dariusza Jasiewicza w Zespole Szkół Technicznych i Ogólnokształcących w Jarosławiu |
| [Zdjęcie udostępnione przez Pana Adama Tomaszewskiego, dyrektora tej szkoły.] |
 |
  |
 |
| Medal i dyplom h.c. Uniwersytetu Andyjskiego w Wenezueli dla Prof. Banacha. |
 |
 |
| Polscy matematycy na znaczkach pocztowych: Zygmunt Janiszewski, Stefan Banach, Stanisław Zaremba i Wacław Sierpiński |
| [z kolekcji prof. Władysława Alexiewicza] |
 |
| Plakat wydrukowany w setną rocznicę urodzin Prof. Banacha. |
,,Banach to niekwestionowana gwiazda polskiej matematyki. Jego imię znane jest wszędzie, gdzie wykłada się matematykę. W czasie swego krótkiego, trwającego zaledwie pięćdziesiąt trzy lata życia (...) umiał godzić potrzeby umysłu płodzącego nieprzerwany strumień genialnych myśli z wielkoświatowym stylem życia, jaki rzadko się spotykało."A Steinhaus swoje przemówienie wygłoszone na uroczystości ku uczczeniu pamięci Stefana Banacha w 1960 roku zakończył słowami:
,, Dał nauce polskiej, a w szczególności matematyce polskiej, więcej niż ktokolwiek inny (...) Łączył w sobie iskrę geniuszu z jakimś zadziwiającym imperatywem wewnętrznym, który mu mówił bezustannie słowami poety: "Jest tylko jedna żarliwa gloria rzemiosła" /Ïl n'y a que la gloire ardente du métier" (Verlaine)/ - A matematycy wiedzą dobrze, że ich rzemiosło polega na tej samej tajemnicy, co rzemiosło poetów."
 |
| Alina Filipowicz-Banachowa |
 |
| Pamiątki po Prof. Banachu w domu Pani Banachowej. |
 |
 Będziemy wdzięczni za wszelkie uwagi i
komentarze dotyczące tej strony.
Będziemy wdzięczni za wszelkie uwagi i
komentarze dotyczące tej strony.