Wortal Stefana Banacha

Polska szkoła matematyczna

Michał Szurek

[PDF]

Młody Technik, nr 11, 27-33 (1978)

To, że Redakcja "Młodego Technika" poprosi kogoś o napisanie artykułu o matematyce polskiej, zostało zdecydowane już... 60 lat temu, (kiedy nie było jeszcze na świecie ani "Młodego Technika", ani autora tego opracowania). Wtedy bowiem zdarzyło się coś niewiarygodnego: w ciągu kilku lat mała i niebogata Polska stała się światową potęgą matematyczną i po dziś dzień matematycy polscy należą do najbardziej cenionych specjalistów. Tak właśnie bywa w nauce, że wybitne umysły pobudzają umysły innych ludzi do wybitnych osiągnięć i raz wzbudzona fala biegnie przez dziesięciolecia. Nikt nie interesowałby się dzisiaj matematyką polską, gdyby nie działalność kilkunastu (a potem kilkudziesięciu) wybitnie uzdolnionych i energicznych osób w początkowych latach niepodległości Polski. Eksplozja matematyki w Polsce - w kraju, który nie miał tradycji w tej dziedzinie wiedzy, i w okresie, gdy kraj nasz po wyjściu ze 123-letniej niewoli i czteroletniej wyniszczającej wojny znajdował się w szczególnie trudnej sytuacji - była czymś fenomenalnym. O niej opowiada ten artykuł.

Aż do końca XIX wieku polski wkład do matematyki światowej był znikomy, choć Józef Maria Hoene-Wroński (1778-1853) wszedł do historii matematyki dzięki wartościowemu zastosowaniu pewnych wyznaczników funkcyjnych do teorii równań różniczkowych (dziś te wyznaczniki są nazywane wrońskianami). Polacy nie uczestniczyli czynnie we wszechstronnym i ogromnym rozwoju matematyki, jaki dokonał się w drugiej połowie XIX wieku. Ileż to wybitnych dzieł literatury polskiej powstało wtedy, gdy język polski był dyskryminowany! W tym samym czasie twórczość matematyczna Polaków była znikoma, niewiele znacząca.

Na krótko przed wybuchem pierwszej wojny światowej sytuacja uległa zmianie. Pojawili się uczeni o znaczniejszej wiedzy, zaczęła się poważniejsza działalność wydawnicza i organizacyjna, inspirowana głównie przez Samuela Dicksteina (1851-1939), a także częściowo finansowana przez niego z własnej kieszeni. Wkrótce zaczęły się ukazywać wartościowe prace z rozmaitych działów matematyki klasycznej, w szczególności prace Stanisława Zaremby (1863-1942) i Kazimierza Żorawskiego (1866-1953). Ponieważ szkoły wyższe w zaborach rosyjskim i pruskim służyły rusyfikowaniu i germanizowaniu Polaków, były one bojkotowane przez patriotycznie usposobioną młodzież. Wielu zdolnych absolwentów gimnazjów z obydwu tych zaborów wyjeżdżało na studia za granicę: bądź do ówczesnej Galicji (do Krakowa lub Lwowa), bądź też na zachód do Francji, Belgii i Anglii, a z zaboru rosyjskiego również do Niemiec. Te studia zagraniczne zaważyły w dużym stopniu na zainteresowaniach, umysłowości i dojrzałości ówczesnych młodych polskich naukowców. Wszyscy późniejsi założyciele polskiej szkoły matematycznej studiowali dłużej lub krócej za granicą: Mazurkiewicż, Steinhaus i Sierpiński w Getyndze, Janiszewski w Paryżu, Kuratowski w Glasgow.

Zainteresowania wymienionych polskich matematyków skierowały się ku nowemu (bo powstałemu w końcu XIX wieku) działowi tej nauki - teorii mnogości (dziś mówimy: teoria zbiorów) i jej zastosowaniom, przede wszystkim topologii. W 1908 roku rozpoczął wykłady jako docent Uniwersytetu Lwowskiego Wacław Sierpiński (1882-1969). W ł909 roku wygłosił on pierwszy na świecie roczny wykład poświęcony teorii mnogości, a w kilka lat później wydał podręcznik z tego zakresu (także pierwszy w świecie), W 1912 roku w Paryżu obronił pracę doktorską Zygmunt Janiszewski (1888-1920), a w 19l3 roku u Sierpińskiego doktoryzował się (na podstawie pracy z topologii) Stefan Mazurkiewicz (1888-1945). Ci uczeni odegrali później najpoważniejszą rolę w powstaniu w odrodzonej Polsce silnej szkoły matematycznej.

W sierpniu 1915 roku wojska carskie opuściły Warszawę, a już w listopadzie otwarto dwie wyższe polskie uczelnie: Uniwersytet i Politechnikę Warszawską. Wśród wykładowców matematyki na Uniwersytecie znaleźli się m.in. Janiszewski, Mazurkiewicz i Sierpiński. Mazurkiewicz był świetnym wykładowcą i bardzo aktywnym badaczem naukowym, Janiszewski nie ustępował mu wiedzą ani pomysłowością, a górował dokładnością, ścisłością i uporządkowaniem wewnętrznym. Obaj poświęcali się przede wszystkim topologii. Sierpiński był już wtedy znanym specjalistą z teorii mnogości i teorii liczb. Algebrę wykładał Dickstein, który szczególnie potrafił zarazić swym entuzjazmem i pasją młodych adeptów matematyki. Zagraniczne studia wpłynęły dodatnio na dojrzałość młodzieży, a atmosferę podgrzewała świadomość, że wszyscy, słuchacze i wykładowcy, są pierwszymi po ponad wiekowej przerwie, którym dane jest uczyć się i nauczać w polskiej wyższej uczelni.

Na początku 1918 roku można było już mówić o dość silnym warszawskim ośrodku naukowym, w którym zajmowano się teorią mnogości i topologią i ich zastosowaniami. Tacy młodzi studenci, jak Bolesław Knaster, Stanisław Saks, Antoni Zygmund, Kazimierz Kuratowski, Alfred Tarski, Kazimierz Zarankiewicz, osiągają wkrótce znaczne i liczące się w skali europejskiej wyniki.

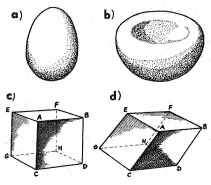Przykład przekształceń topologicznych powierzchni: sferę można przekształcić w powierzchnię o kształcie jajka (a), w powierzchnię o kształcie zgniecionej piłki (b), w sześcian (c), w pewną deformację sześcianu (d). Każda z tych powierzchni jest topologicznie równoważna z pozostałymi oraz ze sferą.

Torus ("obwarzanek") i torus podwójny ("precel") są przykładami powierzchni topologicznie nierównoważnych ze sferą.

O teorii mnogości już wspominaliśmy, jest to po prostu teoria zbiorów. A czym jest topologia? Niech będą dane dwie figury podobne, na przykład dowolny trójkąt w trójkąt tego samego kształtu, ale mniejszy. Każdy z nich można uważać za pewną deformację lub przekształcenie pozostałego, przy czym przekształcenie polega bądź na równomiernym powiększaniu mniejszego trójkąta, bądź też na ściskaniu większego. Gdy dopuścimy i inne sposoby przekszatłcania (na przykład rzutowanie), to trójkąt może przekształcić się na zupełnie inny, pozostanie jednakże trójkątem. Można dokonywać przekształceń jeszcze bardziej istotnych. Na przykład zgniatając koło można je przekształcić w elipsę lub jakiś skomplikowany twór, zaś rozciągając sferę możemy otrzymać np. jajko. Dla niektórych celów, okazuje się wystarczające, by koło można było zastąpić elipsą, a sferę powierzchnią w kształcie jajka. Otóż w latach pięćdziesiątych zeszłego stulecia matematyk niemiecki Riemann pracował nad zagadnieniami z zakresu teorii funkcji zmiennej zespolonej i w celu przedstawienia tych funkcji wprowadził klasę powierzchni, zwanych dziś właśnie powierzchniami Riemanna. Udowodnił, że własności tych funkcji pozostają w ścisłym związku z własnościami geometrycznymi odpowiednich powierzchni, przy czym istotny był tylko "ogólny kształt" danej powierzchni, na przykład koło, elipsa i każda krzywa zamknięta, nie przecinająca się ze sobą, były całkowicie równouprawnione, podobnie jak sfera i jajko. Z drugiej strony, koło i krzywa w kształcie ósemki nie były liniami wymiennymi, podobnie jak sfera, obwarzanek i podwójny obarzanek (precel) nie były wymiennymi powierzchniami. Wobec tego Riemann skierował swoją uwagę na przekształcenia pozwalające na rozciąganie, wyginanie, ściskanie i skręcanie danej figury. Niedozwolone było na przykład rozrywanie. Zapoczątkował tym topologię - gałąź matematyki badającą, jakie własności figur nie zmieniają się przy wymienionych typach przekształceń.

Powstanie w Polsce grupy aktywnie pracującej w jednej (i ponadto młodej i ważnej) dziedzinie było jednym z czynników umożliwiających właśnie rozwój polskiej szkoły matematycznej. To, że grupa ta mogła stworzyć taką "szkołę", było wynikiem nie tylko faktu zebrania się wielu utalentowanych matematyków, ale i tego, że ci ludzie chcieli i umieli ze sobą współpracować, że wysunięto szczęśliwe pomysły organizacyjne, że stworzony został pewien wyraźny program działania i że działalność naukowa objęła przyszłościowy wówczas dział matematyki.

Na polu organizacyjnym największe zasługi położył Janiszewski. Otóż w 1917 roku Kasa im. Mianowskiego, patronująca wówczas polskim naukowcom (zwłaszcza z zaboru rosyjskiego), rozpisała ankietę o potrzebach nauki w Polsce, a u progu niepodległości w 1918 roku wydała tom pod tytułem "Nauka polska, jej potrzeby, organizacja i rozwój", zawierający odpowiedzi na tę ankietę. W tomie tym znalazł się siedmiostronicowy artykuł Janiszewskiego o potrzebach polskiej matematyki. Artykuł okazał się głęboko słuszny i proroczy. Janiszewski sformułował główny cel, do jakiego powinni dążyć polscy matematycy: stworzenie w niepodległej ojczyźnie ośrodka twórczej pracy matematycznej o międzynarodowej renomie. Jednym z zasadniczych środków, zaproponowanych przez Janiszewskiego dla osiągnięcia tego celu, było właśnie skupienie się na niewielkim wycinku matematyki (w którym już i tak zaczynaliśmy się liczyć). Najbardziej nowatorskim pomysłem Janiszewskiego była propozycja wydawania czasopisma poświęconego wyłącznie tym działom matematyki, które miały stanowić podstawowy kierunek badań w Polsce, przy czym artykuły miały być drukowane w językach obcych (to jest głównie niemieckim, francuskim, angielskim i włoskim). "Chcąc zdobyć sobie odpowiednie stanowisko w świecie naukowym, przyjdźmy z własną inicjatywą" - pisał Janiszewski,

Rewolucyjność pomysłów Janiszewskiego zasadzała się na dwóch sprawach. Po pierwsze, do tej pory nie było na świecie ani jednego czasopisma poświęconego wyłącznie tylko wybranym działom matematyki. Większość uczonych w Polsce i za granicą twierdziła, że czasopismo takie nie może utrzymać się jako periodyk naukowy z powodu braku dostatecznej liczby artykułów na odpowiednim poziomie. Obawy takie wyraził na przykład jeden z najbardziej znanych matematyków francuskich, Lebesgue, w liście do Sierpińskiego. Później okazało się, że rozwój matematyki, a topologii w szczególności, spowodował, że poziom publikowanych prac nie maleje, lecz szybko rośnie wskutek konkurencji wśród autorów i sławy, jaką zdobyło polskie czasopismo (nazwane "Fundamenta Mathematicae"). Po dziś dzień pełni ono zamierzoną rolę i zamieszczenie swego artykułu w "Fundamentach" jest ważne dla polskich matematyków.

Drugim nowatorskim czynnikiem w pomysłach Janiszewskiego było to, że prace w "Fundamentach" (nawet polskich autorów) drukowane będą w obcych językach. Niełatwo było przekonać wszystkich, dlaczego Polacy mogą i powinni publikować swe wyniki nie po polsku. Nie zapominajmy, że było to w okresie, gdy narodowi polskiemu przestano utrudniać posługiwanie się własnym językiem! Jednakże środowisko matematyczne zrozumiało, że takie rozwiązanie jest konieczne, zwłaszcza że wiele cennych prac Zaremby i Żorawskiego przepadło dla nauki światowej tylko wskutek opublikowania ich wyłącznie po polsku. Częstokroć udowodnione po raz pierwszy przez Polaków twierdzenia odkrywano na nowo w innych krajach i nowi odkrywcy zyskiwali miano pionierów.

Janiszewski padł ofiarą szczególnie ostrej grypy, jaka nawiedziła Europę w 1920 roku, i nie dożył nawet wydania pierwszego tomu, "Fundamenta Mathematicae", ale jego koncepcje, poparte przez Sierpińskiego, Mazurkiewicza i innych, znalazły szybko oddźwięk w całym kraju. W 1919 roku powstało w Krakowie Towarzystwo Matematyczne, które rychło objęło swym zasięgiem cały kraj. Powstały ośrodki badawcze w Wilnie i Poznaniu, rozwinął się znany już przed wojną ośrodek lwowski. W zamian za "Fundamenta Mathematicae" matematycy polscy otrzymywali inne periodyki z całego świata, co umożliwiło intensyfikację wymiany myśli naukowej z zagranicą (w niezbyt bogatej Polsce wczesnych lat dwudziestych nie można było sobie pozwolić na kupno wszystkich liczących się pozycji). W 1922 roku zaczęto wydawać po francusku roczniki Polskiego Towarzystwa Matematycznego, a wkrótce i inne pozycje. Wszystko to umacniało pozycję Polaków w świecie matematycznym.

Ale złoty okres dla matematyki polskiej rozpoczął się w chwili, gdy w połowie lat dwudziestych we Lwowie powtórnie doszło do "wybuchu" myśli matematycznej. Matematycy lwowscy ograniczyli się (podobnie jak warszawscy) do jednej gałęzi matematyki - analizy funkcjonalnej. Ta tematyka była odmienna od warszawskiej, choć jednak z nią powiązana. Wspaniały rozwój tej gałęzi matematyki w Polsce i na świecie zawdzięczamy głównie Hugonowi Steinhausowi (1887-1972), Stefanowi Banachowi (1892-1945), Stanisławowi Mazurowi (1905-1981), Władysławowi Orliczowi (1903-1990), Juliuszowi Schauderowi (1896-1943) i ich uczniom. Chociaż podstawowe pojęcia analizy funkcjonalnej znane były na początku XX wieku, a nawet wcześniej, to jednak dopiero dzięki pracom Banacha problematyka ta stała się jedną z centralnych dyscyplin nowoczesnej matematyki. Dzisiaj przydaje się ona nie tylko matematykom, ale ma także kapitalne znaczenie dla fizyki (w szczególności dla mechaniki kwantowej) i jej zastosowań.

Napisana przez Banacha w 1929 roku monografia o "operacjach liniowych" była pierwszym na świecie podręcznikiem analizy funkcjonalnej, ugruntowała sławę autora i reprezentowanego przezeń środowiska na wiele, wiele lat. Myślą przewodnią analizy funkcjonalnej jest jakby geometryzacja analizy matematycznej. Jak pary czy trójki liczb można traktować jako punkty (odpowiednio płaszczyzny i przestrzeni trójwymiarowej), tak i bardziej skomplikowane twory: ciągi nieskończone, funkcje itp., można uważać za pewne punkty. Oczywiście, nie są to już punkty zwykłej przestrzeni trójwymiarowej, ale pewnych przestrzeni wielo, a nawet nieskończenie wielowymiarowych. Niektóre takie przestrzenie wyodrębnił właśnie Banach i dziś na całym świecie noszą one nazwę przestrzeni Banacha. Jest to jedno z najczęściej używanych pojęć w matematyce i osoba, która nie wie, co to jest przestrzeń Banacha, pod żadnym pozorem nie może uchodzić za matematyka. Dzięki geometryzacji, o której mowa, rozmaite twierdzenia ściśle analityczne (np. o równaniach różniczkowych) dadzą się ściśle dowodzić metodami najzupełniej geometrycznymi. Odpowiednio patrząc na fakt, że gdy rozciągnięty kawałek gumy wraca do pierwotnego położenia, to chociaż jeden punkt nie zmienia swojego miejsca - można udowodnić twierdzenie o istnieniu rozwiązań szerokiej klasy równań różniczkowych czy całkowych. Dodajmy, że przestrzenie Banacha pozwalają jednocześnie podchodzić do zagadnień analizy metodami algebraicznymi, bo na "punktach" tych przestrzeni rachuje się zgodnie z prawami zwykłego rachunku wektorów. Właśnie zręczne połączenie metody algebraicznej i topologiczno-geometrycznej jest charakterystycznym rysem metody Banacha.

Teorię, którą stworzył Banach, próbowali zbudować wielcy i mali matematycy przed nim. Najbliższy sukcesu był późniejszy twórca cybernetyki, Norbert Wiener, który niezależnie od Banacha osiągnął początkowe sukcesy w tworzeniu podstaw analizy funkcjonalnej. Rezultaty Wienera były tak poważne, że odpowiednie przestrzenie przez pewien czas nosiły nazwę przestrzeni Banacha-Wienera. Jednakże później Wiener doszedł do wniosku, że teoria ta jest tylko czczym formalizmem, że nie odegra żadnej znaczącej roli w matematyce, i zajął się czym innym. W wydanej w 1956 roku swojej autobiografii przyznał, jak bardzo się pomylił. " Teoria Banacha dopiero teraz zaczyna w pełni rozwijać swoją pełną skuteczność jako metoda naukowa" pisał Wiener.

Stefan Banach został odkryty dla matematyki w sposób jakby żywcem wyjęty z dziewiętnastowiecznej powieści obyczajowej lub współczesnej powieści science-fiction. Pisze Hugo Steinhaus:

,,Idąc letnim wieczorem 1916 roku wzdłuż Plant usłyszałem rozmowę, a raczej tylko kilka słów; wyrazy "całka Lebesgue'a" były tak nieoczekiwane, że zbliżyłem się do ławki i zapoznałem z dyskutantami: to Stefan Banach i Otto Nikodym rozmawiali o matematyce. Powiedzieli mi, że mają jeszcze trzeciego kompana, Wilkosza. (...) Niepewność jutra, brak sposobności pracy zarobkowej i brak kontaktu z uczonymi zagranicznymi i nawet polskimi - taka była atmosfera krakowska w 1916 r. Ale to nie przeszkadzało owej trójce przesiadywać w kawiarni i rozwiązywać zagadnień w tłoku i zgiełku. Hałas ich nie odstraszał, a Banach nawet (nie wiadomo dlaczego) wybierał chętnie stoliki blisko orkiestry"

Steinhaus zaprosił obu młodzieńców do swego mieszkania i w trakcie długiej rozmowy opowiedział im o problemach, nad którymi od dłuższego czasu bezskutecznie pracował. W kilka dni później Banach przyniósł gotowe rozwiązanie.

W 1920 roku Banach objął asystenturę na Uniwersytecie Lwowskim (nie mając ukończonych studiów). W tym samym roku przedstawił rozprawę doktorską, a w 1922 roku habilitował się i bezpośrednio potem został mianowany profesorem (znowu za specjalnym pozwoleniem władz państwowych i wbrew zwyczajom akademickim), a w 1924 roku był już członkiem-korespondentem Polskiej Akademii Umiejętności. Do 1939 roku zdołał opublikować ponad 50 prac z różnych działów matematyki. Zmarł na raka i wycieńczony przeżyciami wojennymi, 31 sierpnia 1945 roku.

Oryginalną osobliwością lwowskiej szkoły matematycznej było życie kawiarniane (które, jak widzieliśmy, Banach lubił i przedtem). W ogóle w dawnej Galicji życie kawiarniane odgrywało zdecydowanie pozytywną i inspirującą rolę (w kabarecie "Zielony Balonik" w cukierni Michalika w Krakowie zaczęła się kariera literacka Boya-Żeleńskiego opowiedzenie "kawiarniany inteligent" nie zawierało nic pejoratywnego).

Posiedzenia matematyczne we Lwowie odbywały się w położonych w pobliżu Uniwersytetu kawiarniach, najpierw w "Romie", potem w "Kawiarni Szkockiej". Do licznych zalet tej kawiarni należało serwowanie wyśmienitych ciastek (właściciel utrzymywał, że codziennie ekspediuje je samolotem ze Lwowa do Warszawy) oraz... marmurowe blaty stolików, na których można było szybko pisać i, co ważniejsze, szybko ścierać. Wielogodzinne dyskusje wytwarzały atmosferę wytrwałości, podniecenia, koncentracji i wspólnoty myślowej. Jeden z najwybitniejszych przedstawicieli lwowskiej szkoły matematycznej, Stanisław Ulam, który po wojnie zasłynął w Stanach Zjednoczonych swym czynnym udziałem przy konstrukcji bomby atomowej (a później przy pierwszych maszynach liczących), napisał w 1963 roku: " Jedynym wypadkiem, gdy spotkałem się z podobną Jak we Lwowie wspólnotą zainteresowań, częstotliwością dyskusji i intensywnością współżycia intelektualnego, był okres mych badań nad energią jądrową w czasie wojny".

Stolik, przy którym siadywali Stanisław Ulam, Stanisław Mazur i Stefan Banach, należał do "najsilniejszych" stolików "Kawiarni Szkockiej". Rezultaty dyskusji zapisywano ołówkiem chemicznym na blatach i następnego dnia uczestnicy dyskusji zjawiali się z karteczkami w ręku i (już na trzeźwo, w przenośnym i dosłownym sensie) próbowali odcyfrować swoje wczorajsze gryzmoły i uporządkować je w logiczną całość. Trzeba stwierdzić z żalem, że wiele cennych osiągnięć Banacha i jego uczniów przepadło z wielką szkodą dla nauki polskiej, wskutek braku staranności u adeptów tej szkoły, przede wszystkim zaś samego Banacha. Zresztą gdyby nie pomoc asystentów i przyjaciół, chyba żadna praca Banacha nie dotarłaby do drukarni, tak nieporządną szatą zewnętrzną się odznaczały.

Pewnej jesieni sesja matematyczna w "Kawiarni Szkockiej" przeciągnęła się do... wczesnych godzin przedpołudniowych (dziś wyproszono by ich grzecznie, lecz stanowczo o określonej porze) i jej rezultatem był dowód pewnego ważnego twierdzenia z teorii przestrzeni Banacha, ale gdy szczęśliwi uczestnicy sesji zapisali go chemicznym ołówkiem na blacie i chwiejnym krokiem udali się do domów na zasłużony odpoczynek, nieświadoma niczego sprzątaczka zmyła starannie blat stolika i nie udało się już odtworzyć rozumowania. Toteż wielką zasługą żony Banacha było zakupienie grubego zeszytu o twardych okładkach i powierzenie go płatniczemu w "Kawiarni Szkockiej" z poleceniem wydawania go na życzenie każdemu matematykowi. W ciągu kilku lat powstała z tego zeszytu tak zwana dziś "Księga Szkocka", zawierająca zbiór problemów, jakie matematycy lwowscy stawiali sobie nawzajem (a zarazem i całemu światu) i rozwiązania tych problemów. Każdy, kto stawiał problem, fundował nagrodę dla odkrywcy rozwiązania. Nagrody były różne - mała kawa, butelka wina lub żywa gęś. "Księga Szkocka" przetrwała szczęśliwie wojnę i znajduje się obecnie w Instytucie Matematycznym PAN. Pomysł posiadania podobnego zeszytu i wpisywania tam problemów i ich rozwiązań przyjął się w wielu ośrodkach akademickich na całym świecie i zwyczajowo taki brulion nazywa się "Księgą Szkocką" (z czego najbardziej dumni są Szkoci).

Nie mniejsze osiągnięcia miała i warszawska szkoła matematyczna. Wacław Sierpiński zasłynął z prac z teorii liczb i teorii mnogości i innych działów matematyki, publikując do końca życia 724 prace i komunikaty, 50 książek i sporą liczbę artykułów popularnych, historycznych, przeglądowych oraz siedem podręczników szkolnych. Kazimierz Kuratowski jest znany jako twórca podstaw nowoczesnej topologii, a Karol Borsuk zyskał światową sławę dzięki pracom z teorii retraktów i punktów stałych. Współcześnie Karol Borsuk jest twórcą topologicznej teorii kształtu, jest to najważniejsze osiągnięcie ostatnich lat z dziedziny topologii. Z badań nad podstawami matematyki zasłynął zmarły niedawno Andrzej Mostowski.

Matematyka polska poniosła wielkie straty w czasie ostatniej wojny, podobnie jak cała nasza nauka i kultura. Okupanci niemieccy zamordowali wielu wybitnych polskich uczonych. Banach i Mazurkiewicz zmarli w wyniku wycieńczenia wojną, wielu profesorów osiadło za granicą. Od przypadkowej bomby w 1942 roku spłonęła całkowicie biblioteka Seminarium Matematycznego w Warszawie, a prywatne zbiory matematyków warszawskich zniszczone zostały w czasie powstania. Niemal wszyscy matematycy warszawscy, którzy przeżyli, pozostali bez jednej książki czy odbitki. Tym niemniej matematyka polska odrodziła się po wojnie i znowu osiągnęła najwyższy światowy poziom.

W 1946 roku, dyrektor departamentu w Ministerstwie Oświaty, Stanisław Skrzeszewski, powiedział: ,,Polska eksportuje węgiel i twierdzenia matematyczne". To zdanie jest i dziś prawdziwe.

Podziękowania

Panu dr. hab. Michałowi Szurkowi z Instytutu Matematyki Uniwersytetu Warszawskiego bardzo dziękujemy za zgodę na umieszczenie na naszej witrynie tego artykułu oraz Panu Adamowi Dębowskiemu, redaktorowi naczelnemu Młodego Technika, dziękujemy za zgodę w imieniu Wydawnictwa ATV Korporacja.

Będziemy wdzięczni za wszelkie uwagi i komentarze dotyczące tej strony.

Emilia Jakimowicz i Adam Miranowicz

File translated from T_EX by T_THgold, version 4.00.
On 04 Jan 2012, 18:53.